ここでは望遠鏡の工作に用いる材料の物理的な性質を実際に測定した結果を示します。 望遠鏡の工作では重心位置の計算、たわみ量の推定、水平・高度軸受けの大きさの検討といった際にこれらのデータが必要になります。
比重
望遠鏡の工作によく使う材質の比重を実際に測定しました。
| 材質 | 比重 [ g/cm3 ] | 測定日 |
|---|---|---|
| アルミニウム(A6061) | 2.7 | 2015年8月21日 |
| 鉄 (ASTM A36) | 7.9 | 2015年9月5日 |
| 材木 (Softwood) (1) | 0.42 | 2015年8月21日 |
| 合板 (Hardwood Plywood) (1) | 0.64 | 2015年8月21日 |
| 合板 (Oak Plywood) (2) | 0.55 | 2015年9月5日 |
| 合板 (Birch Plywood) (2) | 0.51 | 2015年9月5日 |
| 合板 (Baltic Birch Plywood) (3) | 0.68 | 2019年6月1日 |
| 合板 (バーチ耐水合板) (4) | 0.66 | 2024年4月15日 |
- Home Depot で購入(ハワイ州ヒロ)
- Lowes で購入(ハワイ州コナ)
- Woodcraft で購入(通販)
- テツヤ・ジャパン で購入(通販)
合板は材質、販売元(製造元)によって比重が大きく異なることが判りました。 Birch Plywood と Baltic Birch Plywood では、おなじ Birch(樺)でも大きく違うことが判りました。
(参考)比重の測定原理
比重とは単位体積あたりの重量のことです。 比重は測定したい材料を直方体に切り出して幅・奥行き・高さの3辺の寸法と重量の測定から求められます。
ある均一な材質でできた直方体の比重 ρ は、直方体の質量 M 、直方体の大きさ(幅 W 、奥行き D、高さ H)とすると、以下の式で表せます。
![]()
私はノギスで寸法を、製菓用の電子秤で重量を測り、比重を求めました。
熱膨張率
望遠鏡の工作によく使う材質の熱膨張率を実験して調べました。
| 材質 | 熱膨張率 [ x 10-6/oC ] | 測定日 |
|---|---|---|
| アルミニウム (A6061) | 15 | 2015年8月21日 |
| 合板 (Hardwood Plywood) (1) | 1.6 | 2015年8月21日 |
| 材木 (Softwood, 繊維と平行) (1) | 5.8 | 2015年8月21日 |
| 材木 (Softwood, 繊維に直交) (1) | 32 | 2015年8月21日 |
- Home Depot で購入(ハワイ州ヒロ)
アルミニウム (A6061) の熱膨張率の実験結果は一般的に知られている値(23 x 10-6/oC)よりも小さい値となりました。理由はよく分かりません。
合板 (Hardwood Plywood) の熱膨張率は方向にかかわらず、かなり小さい値であることが判りました。 これは熱膨張率の小さい光学ガラス(パイレックス 3.3 x 10-6/oC、溶解石英 0.55 x 10-6/oC)とほぼ同等の熱膨張率です。 光学系と接するところなど、使い方によっては合板 (Hardwood Plywood) はかなり有用な材料と言えそうです。
(参考)熱膨張率の測定原理
熱膨張率(線膨張率)とは単位長さ当たりの単位温度あたりの長さの変化率のことです。 熱膨張率の測定では、測定したい材料を直方体に切り出し、様々な温度で長さを測定することから求められます。
ここで、均質な材質で出来た直方体について、温度 TA で測定した時の長さを LA、温度 TB で測定した時の長さを LB と書くと、熱膨張率 α は以下の式で書き表すことが出来ます。
![]()
私の行った実験では、冷凍庫、室温、熱湯を用いて温度を変えました。 寸法はノギス、温度は家庭用の温度計を用いて、また熱湯の場合は 100oC として計算しました。
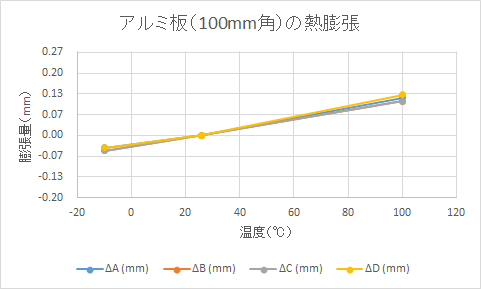
(実験結果1)アルミ (A6061) の熱膨張率の測定実験結果
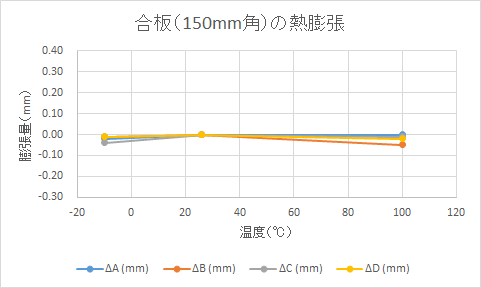
(実験結果2)合板 (Hardwood Plywood) の熱膨張率の測定実験結果
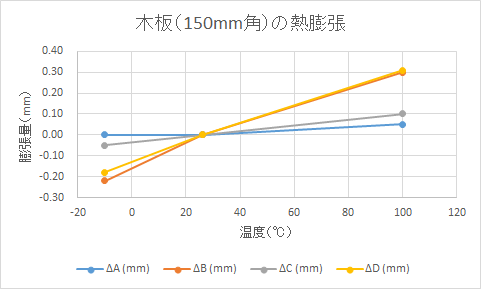
(実験結果3)材木 (Softwood) の熱膨張率の測定実験結果
ヤング率
望遠鏡の工作によく使う材質のヤング率について実験して調べました。
| 材質 | ヤング率 [ x 109 Pa ] | 測定日 |
|---|---|---|
| アルミニウム (A6225) | 60 | 2015年9月6日 |
| 鉄 (ASTM A36) | 180 | 2015年9月6日 |
| 合板 (Hardwood、パネル面に垂直) (1) | 3.5 | 2015年9月6日 |
| 合板 (Oak、パネル面に垂直) (2) | 6.0 | 2015年9月6日 |
| 合板 (Birch、パネル面に垂直) (2) | 3.8 | 2015年9月6日 |
| 合板 (Baltic Birch、パネル面に垂直) (3) | 9.7 | 2020年12月26日 |
| 合板 (バーチ耐水合板、パネル面と平行) (4) | ||
| 合板 (Hardwood、パネル面と平行) (1) | 2.9 | 2015年9月6日 |
| 合板 (Oak、パネル面と平行) (2) | 2.9 | 2015年9月6日 |
| 合板 (Birch、パネル面と平行) (2) | 2.8 | 2015年9月6日 |
| 合板 (Baltic Birch、パネル面と平行) (3) | 6.4 | 2020年12月27日 |
| 合板 (バーチ耐水合板、パネル面と平行) (4) |
- Home Depot で購入(ハワイ州ヒロ)
- Lowes で購入(ハワイ州コナ)
- Woodcraft で購入(通販)
- テツヤ・ジャパン で購入(通販)
合板について、まずハワイ島で容易に入手可能なものを調べました。 合板のパネル面に垂直な方向に荷重をかけた場合、Oak Plywood は他の合板と比べてヤング率が大きく、たわみにくい素材だということが判りました。 比重 も 0.55 g/cm3 と小さく好都合です。 一方でホームセンターで安価に売られている Hardwood Plywood は比重が 0.64 g/cm3 と大きい割にヤング率は小さく、たわみやすい素材であることが判りました。
次に通販で Baltic Barch Plywood を購入してこれを調べました。 合板のパネル面に垂直な方向に荷重をかけた場合、Baltic Barch Plywood のヤング率は 9.7 x 109 Pa と他の合板と比べて1.5~3倍近く大きく、たわみにくい素材だということが判りました。 木工工作をしている感触でも、硬く、切りにくい印象です。 比重が 0.68 g/cm3 と少し大きいのが欠点ですが、比重の割にヤング率は大きく、強度(たわみが少ないこと)が求められる部分には Baltic Barch Plywood が良いと言えます。
パネルと平行な方向のヤング率を調べたところ、合板はパネルに垂直な方向と平行な方向とではヤング率が違うことがわかりました。 合板の向きは注意して設計・使用する必要があることがわかりました。 また、ここでも Baltic Barch Plywood は他の合板の2倍以上大きく、たわみにくいことが判りました。
(参考)ヤング率の測定原理
ヤング率とはフックの法則が成り立つ範囲における物質の変形しにくさを表す係数のことで、フックの法則の「バネ係数」に相当するものです。 金属や木材などは力(圧力)がある程度の範囲内であればバネのように弾性変形し、力(圧力)がなくなれば元の形に戻ります。 この時の変形しにくさを表す量がヤング率になります。
ヤング率はある物質を単位長さだけ変形させるときに必要な単位断面積あたりの力(圧力)となります。 曲がりにくい物質、たわみにくい物質ほどヤング率は大きな値となります。
私の実験では、材料を細長く加工して片持ち梁とし、その先端に加重を加えた時のたわみ量を測定することでヤング率を求めました。 先端荷重のかかる片持ち張りのたわみ量 σ は 加重 F 、梁の長さ l、ヤング率 E、二次断面モーメント I から以下の式で求めることができます。
![]()
この式を解いて、ヤング率 E は以下の式となります。
![]()
私の実験では、幅約5cm、長さ約120cmの材料を用意し、一端を自宅に建て付けの本棚に固定して、もう一端におもりをぶら下げて実験しました。 寸法はノギスと巻き尺、重量は製菓用の電子はかりで測定しました。

2. 合板の継ぎ足し
ハワイ島で比較的容易に手に入る合板で最もたわみにくい材料は Oak Plywood でした。 しかしこの合板は 1/2 インチ厚、縦横 2 ft x 4 ft のものしか手に入りません。 そこで 2 枚を木工ボンドで貼り合わせて継ぎ足して使用できないか、実験して確かめることにしました。
実験の結果、この場合のヤング率は約 2/3 に低下することが判りました。 接着剤を変更したり断面を工夫すれば改善はあると思いますが、素人工作では合板の継ぎ足しは避けるのが無難と思いました。
| 材質 | ヤング率 [ x 109 Pa ] | 測定日 |
|---|---|---|
| 合板 (Oak Ply、パネル面に垂直) (2) | 3.9 | 2015年9月14日 |
| 合板 (Oak Ply、パネル面と平行) (2) | 2.5 | 2015年9月14日 |
- Lowes で購入(ハワイ州コナ)

2. ヤング率と二次断面モーメントの積
実際の工作ではヤング率よりもヤング率 E と二次断面モーメント I の積 E x I のほうが便利な場合もあります。 特に鉄角パイプ、アルミ丸パイプなどの複雑な形の「実際の」二次断面モーメントを求める事は難しいと思います。 そこでよく使う部材のヤング率と二次断面モーメントの積 E x I を測定しました。
| 材質 | E x I [ N・m2 ] | 測定日 |
|---|---|---|
| 1" 鉄角パイプ (1/16"厚) | 1200 | 2015年9月6日 |
| 1" アルミ丸パイプ (1/16"厚) | 410 | 2015年9月6日 |
1" 鉄角パイプ (1/16"厚) の実験結果は一般に知られている鉄のヤング率と理想的な形状の二次断面モーメントの積の値(2600N・m2)と大きく異なりました。理由はよく分かりません。
摩擦係数
実験に基づいて、望遠鏡の工作によく使うであろう組み合わせの静止摩擦係数・動摩擦係数を調べました。
| 材質の組み合わせ | 静止摩擦係数 | 動摩擦係数 | 測定日 |
|---|---|---|---|
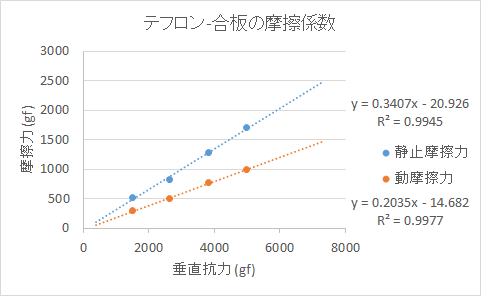
| テフロンと合板 | 0.34 | 0.20 | 2015年9月6日 |
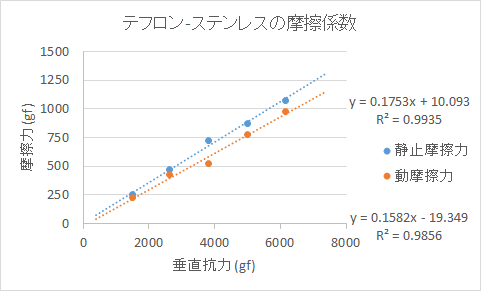
| テフロンとステンレス | 0.18 | 0.16 | 2015年9月13日 |
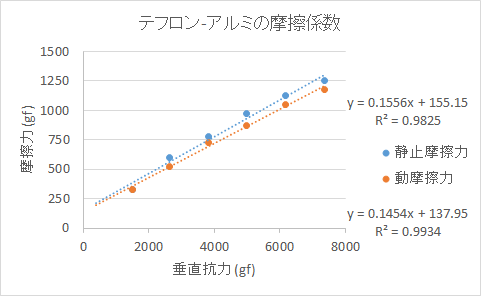
| テフロンとアルミ | 0.16 | 0.15 | 2015年9月6日 |
| テフロンとFRP | 0.10 | 0.093 | 2015年9月6日 |
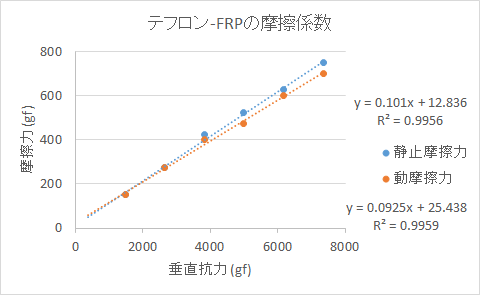
静止摩擦係数と動摩擦係数の差が小さい組み合わせがドブソニアンの軸受けとして適しています。 また静止摩擦係数・動摩擦係数共にその値が小さい方が軽い力で動かす事が出来て好都合です。 実験した組み合わせでは、テフロンとFRPの組み合わせが最も適していることが判りました。
ちなみに Portable Newtonian Telescope によると、テフロン (PTFE) と Wilsonart社のラミネート Ebony Star #50 (4552-350-50) の組み合わせが最もドブソニアンの軸受けとして適しているとのことです。 しかし残念なことに #50 のエボニースターは製造が中止され、2015年現在入手できません。 粒度の異なる #90 (4552-350-90) も適しているそうですが、これも私の調べた限り入手できませんでした。 他の粒度の異なる Ebony Star は入手可能ですが、これらはドブソニアンのベアリングとしては適していないそうです。
さらに Portable Newtonian Telescope によると、FRPのパネル(浴室などで使われる表面が凸凹しているもの)が Ebony Star #50 の代用として使えると紹介されています。 このFRPパネルは米国では Home Depot 等のホームセンターでどこでも売られているもので、安く簡単に入手できます。 (4 ft x8 ft のシートで売られているので運ぶのが大変ですが。) 表面は鮫肌で凸凹しています。 このFRPボードの元々の使用用途は浴室の内壁パネルのようです。 日本で同等のものが手に入るかわかりませんが、触った感触としては浴室の床材に使われている凸凹とした大理石のような肌触りです。

1. 静止摩擦係数の測定原理
摩擦力とは2つの物体が接している時にその接触面に平行に働く力のことです。 2つの物体に垂直にかかる力を Fw、水平にかかる摩擦力を Ff と書くと、摩擦係数 μ は以下の計算式で書き表すことができます。
![]()
静止摩擦力とは物体が静止した状態で生じる最大の摩擦力のことです。 この時の摩擦係数を「最大静止摩擦係数」、または単に「静止摩擦係数」と呼びます。 静止摩擦係数から物体が動き始める瞬間に必要な力を計算することができます。
実際の実験では2つの物体に垂直にかかる力をいろいろ変えながら、物体が動き始める瞬間の摩擦力を「バネばかり」を使って測定することで求めました。
2. 動摩擦係数の測定原理
動摩擦力とは物体が動いているときに生じる摩擦力のことです。このときの摩擦係数を「動摩擦係数」と呼びます。 動摩擦係数から物体が動いているときに必要な摩擦力を計算することができます。
実際の実験では2つの物体に垂直にかかる力をいろいろ変えながら、物体を等速直線運動させているときの摩擦力を「バネばかり」を使って測定することで求めました。
3. テフロンと合板の摩擦係数の測定実験結果
4. テフロンとステンレスの摩擦係数の測定実験結果
5. テフロンとアルミの摩擦係数の測定実験結果
6. テフロンとFRPの摩擦係数の測定実験結果