分解能について肉眼の場合と望遠鏡を用いた場合の両方について考察します。なおここでは空の明るさやシーイングといった環境の影響はないものと仮定し、望遠鏡も無収差円形開口の理想的な場合を仮定して議論を進めます。
視力（明るい恒星の場合）
明るいところでの肉眼の分解能は「視力」として一般に表されます。
まとめ：明るいところでは肉眼の分解能は「視力」として定義され、 視力 1 で分解能 1 [分角] となる。 明るい恒星の場合、視力 1 のヒトの肉眼での分解能は 1 [分角] となる。
視力とは分解能の逆数で、視力 1 が分解能 1 [分角] に相当します。 視力には個人差があります。 良い人は視力 2 = 分解能 0.5 [分角]、運転免許取得に必要な視力は 0.3 = 分解能 3.3 [分角] です。 視力には個人差がありますが、私のウェブサイトでは視力 1 = 分解能 1 [分角] を標準的な視力として、以下考える事にします。
ちなみにヒトの目の性質に書いたように、明るいところではヒトの目は錐体がその視覚を司っています。 錐体にのみ色が判別出来る事から、色が見えるような明るい光源すなわち明るい恒星の場合は視力 1 のヒトの肉眼での分解能は 1 [分角] あることになると考えられます。
肉眼の分解能 (暗い恒星の場合)
まとめ：恒星といった暗い点光源を見る場合、肉眼の分解能は 10 [分角] と推定される。明るい星の場合と比べ、 10 [倍] 悪い（大きい）分解能となる。
暗いところでの肉眼の分解能は経験上、明らかに「視力」よりも低下します。 例えばおおぐま座のミザールとアルコルは離角 12 [分角] の2重星です。 古代エジプトではこの2重星を兵士の視力検査に用いたと言う話を良く聞きますが、もし明所での視力でそのまま計算すると、ミザールとアルコルが分離できるギリギリの視力は 0.08 となってしまいます。 非常に視力の悪い兵士を調べることが目的だったのなら納得いきますが、視力検査としては適してないでしょう。 自分の目で確かめたところ、裸眼視力 0.3 では分離できず、補正視力 1.2 では分離できました。
そこで、ヒトの目の性質に書いたように、暗所での視覚は桿体が司ることになります。 桿体は分解能が悪い代わりに感度が高く、色を認識できません。 私の経験上、暗い星は色が判別出来ません。これは暗い星は桿体で認識しているからだと考えられます。 同様に考えると、ミザールとアルコルについても星の色が見えないことから桿体で見えていると考えられます。 桿体で見えているため分解能は悪く、（明視）視力 0.3 では分離できず（明視）視力 1.2 では分離できたのでしょう。
上記の経験から、私は視力 1 程度の人の暗所での肉眼分解能はおよそ 10 [分角] 程度だと推定します。
肉眼の分解能 (淡く広がった天体の場合)
まとめ：淡く広がった天体の場合、肉眼の分解能は 1.5 [度] = 90 [分角] と推定される。明るい恒星の場合の 90 [倍]、暗い恒星の場合の 9 [倍] 悪い（大きい）分解能となる。
文献調査
臼井正（2007）によると非常に淡い天体の場合、天体の大きさが数度を超えると天体が見えるか見えないかは天体の全光度ではなく天体の単位面積当たりの明るさによるとのことです。 これは天体が非常に淡い場合、数度未満の構造は見分けることができないことを意味します。 例えば天の川は肉眼で見えますが、その詳細な形まではよく分かりません。 同様にアンドロメダ銀河やオリオン大星雲も肉眼では見えますがその形まではよく分かりません。 よって淡く広がった天体の場合、肉眼の分解能は数度程度しかないことになります。
室内実験
ここで自分の目で確かめてみました。 次に示すような写真のように、黒い板に白色の丸を貼り付けたものを夜の室内に置き、離れたところからそれを見ることでどの程度視直径であれば「見える」か確かめました。 少しずつ距離を変え、見えなくなった時の距離を記録しました。 実験ではアイピース越しに星を見ることを想定して片目をつぶって測定しました。 また眼鏡の有無も比較しましたが、分解能に違いはありませんでした。
| 白丸の直径 | 白丸までの距離 | 白丸の視直径 | 判定 |
| 20cm | 210cm | 5.4度 | 見える |
| 20cm | 320cm | 3.6度 | 見える |
| 7.5cm | 210cm | 2.0度 | 見える |
| 5cm | 210cm | 1.4度 | 見えない |
| 7.5cm | 320cm | 1.3度 | 見えない |
| 5cm | 320cm | 0.9度 | 見えない |
実験結果から視直径 1.3～1.4 [度] よりも視直径が小さくなると見えないことが判りました。 よって淡く広がった天体の場合の肉眼の分解能は非常に悪いことが文献からも実験からも示されました。 分解能には個人差もあるので、私のウェブサイトではおおざっぱに見積もって、淡く広がった天体の場合の肉眼の分解能は 1.5 [度] = 90 [分角] と推定します。
なお上記の実験の時の白丸の表面輝度は SQM-L で測定して 23.4 [等級/平方秒]、背景の黒い板は 23.6 [等級/平方秒]、部屋の壁は 23.5 [等級/平方秒] で、それぞれ明るさの違いは知覚できました。
参考文献：
- 加藤賢一、「天の川が見える怪」、天文教育、2006年11月号
- 臼井正、「続・天の川が見える怪」、天文教育、2007年3月号
- 吉田正太郎、「天体アマチュアのための新版反射望遠鏡光学入門」、誠文堂新光社、2005年
望遠鏡の分解能 (明るい恒星の場合)
まとめ：望遠鏡を使ってヒトの目で見た場合の明るい恒星の分解能は望遠鏡のレーリー・リミット、すなわち回折限界となる。ただし口径に応じたある倍率でないと分解して見る事は出来ない。 また（この倍率よりも高い倍率であれば）望遠鏡の分解能は倍率に依存しない。
点光源である恒星は面積がないため望遠鏡とアイピースを通して見られる恒星の虚像は望遠鏡の倍率に依らずヒトの目の網膜上の一点で結像する事になります。 よって望遠鏡を使った場合は肉眼の場合と比べて「望遠鏡の集光力」倍の明るさで恒星像を見ることになります。 そのため大多数の恒星像は十分な明るさを持ち、「錐体」で知覚されると考えられます。 錐体で見えると考えると、色を認識でき、また高い分解能で見ることが出来ると考えられます。
望遠鏡を使うことで原理的には倍率は無限に大きくすることが出来ます。 無限に倍率を大きくすることが出来ると言うことは、見かけの大きさは無限に大きく出来る事になります。 そうすると無限に小さい角度まで分解して見る事が出来る事になります。
しかし実際こんなことはなく、光が波の性質を持っていることからくる不定性によって望遠鏡の分解能には限界があります。
これが「レーリー・リミット」または「回折限界」と呼ばれる、望遠鏡の分解能（2点を見分けられる最小の角度）となります。
望遠鏡の分解能 
[radian]は望遠鏡の口径 
、波長 
として以下の式で書くことが出来ます。
波長 555 [nm] (錐体の感度のピーク波長)で計算すると、口径 140 [mm] で分解能は 1.0 [秒角] になります。望遠鏡の分解能は口径に反比例して小さくなるため、口径が大きくなればなるほど細かい構造を見分けることができるようになります。 以下は明るい恒星の場合の望遠鏡の分解能を口径毎にプロットした図です。 口径が大きくなるほど分解能が小さくなる事がわかります。
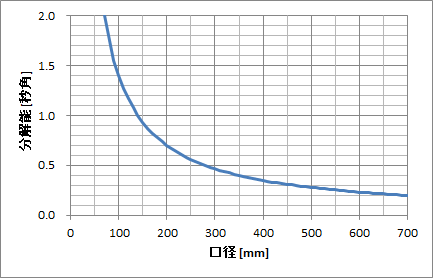
ここで ヒトの目の性質 に書いた「瞳径」について考えます。
ヒトの目の瞳径は暗所ではおよそ直径 7 [mm] まで広がると言われています。
これを上の式に当てはめて計算すると、ヒトの目の理論的な分解能は瞳径 7 [mm] のとき分解能 0.33 [分角]、すなわち視力 3 となることがわかります。
逆に考えると視力 1 の人の場合、瞳はその中心部の 7/3 = 2.3 [mm] の範囲の光だけを使っていることになります（この範囲の瞳しか有効に使えていない）。
そのため上記の望遠鏡の分解能を達成する為には視力 1 の人の場合、望遠鏡の（射出）瞳径が 2,3 [mm] となるような倍率で観察しなければいけないと考えられます。この倍率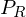 
は望遠鏡の口径 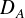[mm] から以下の式で計算されます。
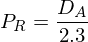
以下は明るい恒星の場合の望遠鏡の分解能と、この分解能を達成するために必要な倍率を口径毎に示した表になります。
| 口径 [mm] | 分解能 [秒角] | 必要倍率 [倍] |
| 100 | 1.4 | 43 |
| 200 | 0.70 | 86 |
| 400 | 0.35 | 170 |
| 600 | 0.23 | 260 |
| 800 | 0.17 | 340 |
さらに考察を進めると、倍率を大きくすると望遠鏡の（射出）瞳径は小さくなり、その結果ヒトの目の分解能は低下すると考えられます。
しかし倍率が大きくなるとそれだけ天体の見かけの大きさも大きくなります。
そのためトータルでは分解できる（実際の）最小離角は一定になるはずです。
よって望遠鏡の理論的な分解能（レーリーリミット）を得るためには上に示した倍率 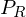以上の倍率が必要ですが、それ以上の倍率であれば分解能は一定で、倍率に依存しないと考えられます。
まとめると、望遠鏡で明るい恒星を見た場合の分解能は望遠鏡の理論的な限界（レーリーリミット）となる。ただし、口径に応じたある倍率 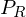以上でないと分解して見る事は出来ない。また 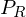よりも高い倍率であれば望遠鏡の分解能は倍率に依存しない。