所有する自作60cmドブソニアンや自作40cmドブソニアンの主鏡の光学性能を評価したいと考え、フーコーテスターを自作し、フーコーテストを行いました。 ここではフーコーテストの原理とテストの結果を紹介します。
- 40cm F4.53 Discovery Telescopes
- 60cm F3.35 Lockwood Custom Optics
- 非点収差の検出
- 60cm F3.25 Lockwood Custom Optics(新)

- 15cm F6.71 自作鏡
フーコーテストの原理
フーコーテストでは焦点距離 f の 2 倍の距離に光源を置き、反射鏡で反射した光をナイフで切ることで反射鏡の局所的な(ある入射高の)曲率半径を測定する技術のことで、一種の「光てこ」です。
まず球面鏡の場合を考えます。 球面鏡は「球心」(鏡から焦点距離 f の 2 倍離れたところ)から出た光は球面鏡のどこで反射しても再び球心に戻ってきます(作図すれば分かる)。 そのため球面鏡でフーコーテストを行うと光源から出た光は球面鏡に反射して再び球心=光源と同じ位置に戻り、1 点で交わります。
次に放物面鏡を考えます。 この場合は球面鏡でないため焦点距離の 2 倍離れたところから出た光はほぼ光源と同じ位置に戻ってきますが、1 点では交わりません。 反射鏡の高さ(入射高)毎に別々の場所に光が集まります。 これは放物面鏡の場合、入射高が高いほど焦点距離が長いためです。 よって入射高 h 毎に光が集まる場所 xk を記録して計算と比較することでどんな形状の反射鏡なのかを推定できます。 これがフーコーテスト(ゾーンテスト)の原理です。
次の図は焦点距離 f の放物面鏡のフーコーテストを示したものです。 ナイフと光源の位置が同じ(一緒に動く)場合、点 K に位置する光源から出た光は反射鏡のある高さ(入射高)h で反射して再び点 K に戻ってくると考えます。
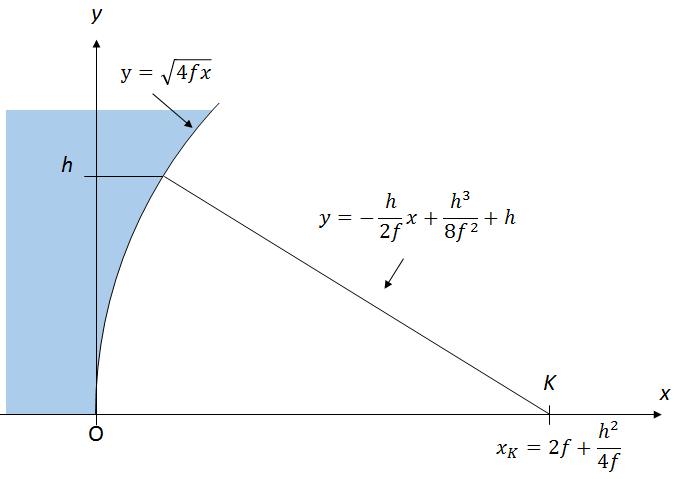
ここでフーコーテスターで測定したナイフ位置 xk と入射高 h を考えます。 実際の望遠鏡の鏡は理想的な放物面からの製造誤差=「ズレ」を持っています。 よって実際の測定結果とこの理論的な計算結果は完全には一致しません。 この理想的な放物面からの「ズレ」から鏡面の「誤差」を見積もっていきます。 このフーコーテストの測定結果と理論位置の差を「ナイフ位置誤差」と呼びます。
次にナイフ位置誤差から縦収差への変換を考えます。 フーコーテストでは焦点距離 f の 2 倍離れたところの光源を見て、その時どれだけナイフ位置がズレるかを測定しました。 しかし実際に私達が知りたいのは無限遠の光源からの光、つまり天体からの光がどのように焦点に集まるか、です。 これは「縦収差」(結像面の前後にズレる収差)と呼ばれる収差に相当します。
検討の結果、「ナイフ位置誤差」から「縦収差」への変換は数値的に計算して推定すればよいと考えました。 数値計算の結果、縦収差はナイフ位置誤差のほぼ 1/2 となることがわかりました(ナイフと光源が一緒に動く場合)。さらに「縦収差」から「波面誤差」へ変換します。 この場合は少し計算が面倒ですが次の図のように考える事で、入射高 h の理想波面と、Δs の球面収差のある入射高 h+Δh の波面のズレ量(=波面誤差Δw)が DE となることがわかります。 図中のそれぞれ点 A, B, C, D, E 座標は直線と曲線の交点を求めることで計算から求められます。 そこから DE の長さを求めます。 さらに計算から求めた DE(Δw)は入射高 h から h+Δh の間の波面誤差となるので鏡全体の波面誤差鏡の中心から縁までの波面誤差を足し合わせる(w = ΣΔw)ことで求められます。
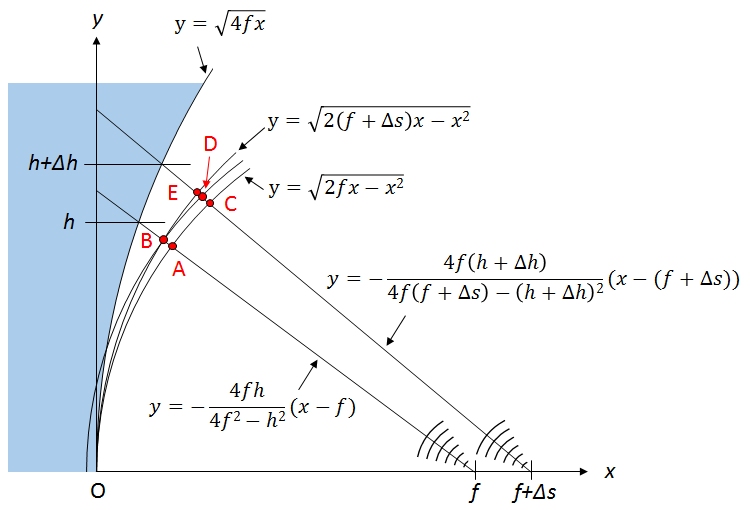
以上まとめると、フーコーテストではまずナイフ位置 xk と入射高 h を測定で求め、次に計算から求められる理想と比較することで「ナイフ位置誤差」を求め、「ナイフ位置誤差」から「縦収差」、「縦収差」から「波面誤差」と変換して、鏡面誤差を求めることになります。
フーコーテストは「光てこ」と言って「光の反射の法則」と「光の直進性」を利用して鏡面の凸凹を非常に大きく拡大して見る技術です。 焦点距離や入射高にも依りますが 0.1 mm のナイフ位置誤差は 10 nm 程度の波面誤差に相当します。 非常に簡単な原理ですが鏡面を約 10,000 倍に拡大して見ていることになります。
自作フーコーテスター
プロクソンのマイクロクロステーブルを使用してフーコーテスターを自作しました。 X, Y に微動できます。 動かした量はアナログのダイヤルゲージで測定します。 60 cm F3.3 放物面鏡の場合は移動量が大きいためダイヤルゲージを2つ使いました。 ナイフと光源は一緒に動かすタイプです。 ナイフはカミソリの刃を買ってそのまま取り付けました。 光源は白色 LED ライトのついたキーホルダーを使用しました。 元々光源にもスリットを設けていましたが、途中からいわゆる「スリットレス」タイプに改造しました。 微動ステージの動きが渋いため、作り直すことにしました。

自作フーコーテスター(新)
自作フーコーテスターの微動ステージの動きが渋かったため自作15cm鏡の研磨に合わせて新たに製作しました。 微動ステージは Amazon.com で見つけた60 mm 角のマイクロステージで X, Y, Z に微動できます。 移動量は分解能 1/1000 mm の分解能のデジタルゲージで測定します。 ナイフと光源は一緒に動かすタイプです。 ピンホールやスリットの無い「スリットレス」タイプのフーコーテスターです。 光源は緑色の高輝度 LED を使用しました。

実際の測定
何回か測定しているうちに、どうすれば測定がうまく行くか分かってきました。 ノウハウを簡単に列記します。
- 写真で判定する
- ゾーンテストは肉眼で見てもよく分からない
- 三脚に固定したカメラ(コンパクトデジカメでもOK)で撮影して Makali`i などの画像解析ソフトを使って影の位置を調べる方法が客観的で正確と思われる
- ただし時間がかかる(測定10分、解析1時間以上)
- 入射高 h を正しく見積もる
- 写真に写る鏡の直径を基準として入射高 h を計算する場合、物理的な鏡の直径(物理口径)と有効口径を区別すること
- 写真に写る鏡はアルミニウムがコーティングされている部分=有効口径の部分のみ
- 当初、写真に写る鏡の直径を物理口径だと考え、それを基準に入射高 h を求めていたため、測定結果がおかしかった
- 測定の直前に鏡面に定規をあててピクセルスケールを調べるのが最も確実と思われる
- 焦点距離 f は別に測定する
- 原理的にはベストフィットから焦点距離 f を求めることもできるが、収差が大きいためなのか、それだとうまくいかなかった
- 軽い角材にメジャーを貼り付けて長さ約 4 m の定規を自作し、これを用いて鏡の中心とナイフとの距離を測定することで焦点距離を測定した
- 測定は深夜に行う
- 夕方だと部屋の床や壁からかげろうが立ち、なかなか像が安定しない
- 測定中は風が吹かないように窓などは締め切って行うのが良い
- コンクリート床のすぐ上は空気の流れがあってダメ、できるだけ床から離した方が気流の影響は少ない
- 鏡の温度が部屋の温度に十分順応してから測定することが重要、セットアップしてから2,3時間は待った方が良い
40cm F4.53 Discovery Telescopes
自作40cmドブソニアン で使用してきた Discovery Telescopes 社製 40cm F4.53 主鏡をフーコーテストしました。
| 物理口径 | 406 mm |
| 有効口径 | 403 mm |
| 焦点距離 | 1824 mm (公称値: 71.5") |
| F値 | 4.53 |
| 鏡材 | Pyrex |
| 製作会社 | Discovery Telescopes |
| 購入年 | 2006年 |
| シリアルナンバー | N/A |
| 測定日 | 2015年5月17日 |
| 測定者 | 沖田博文 |
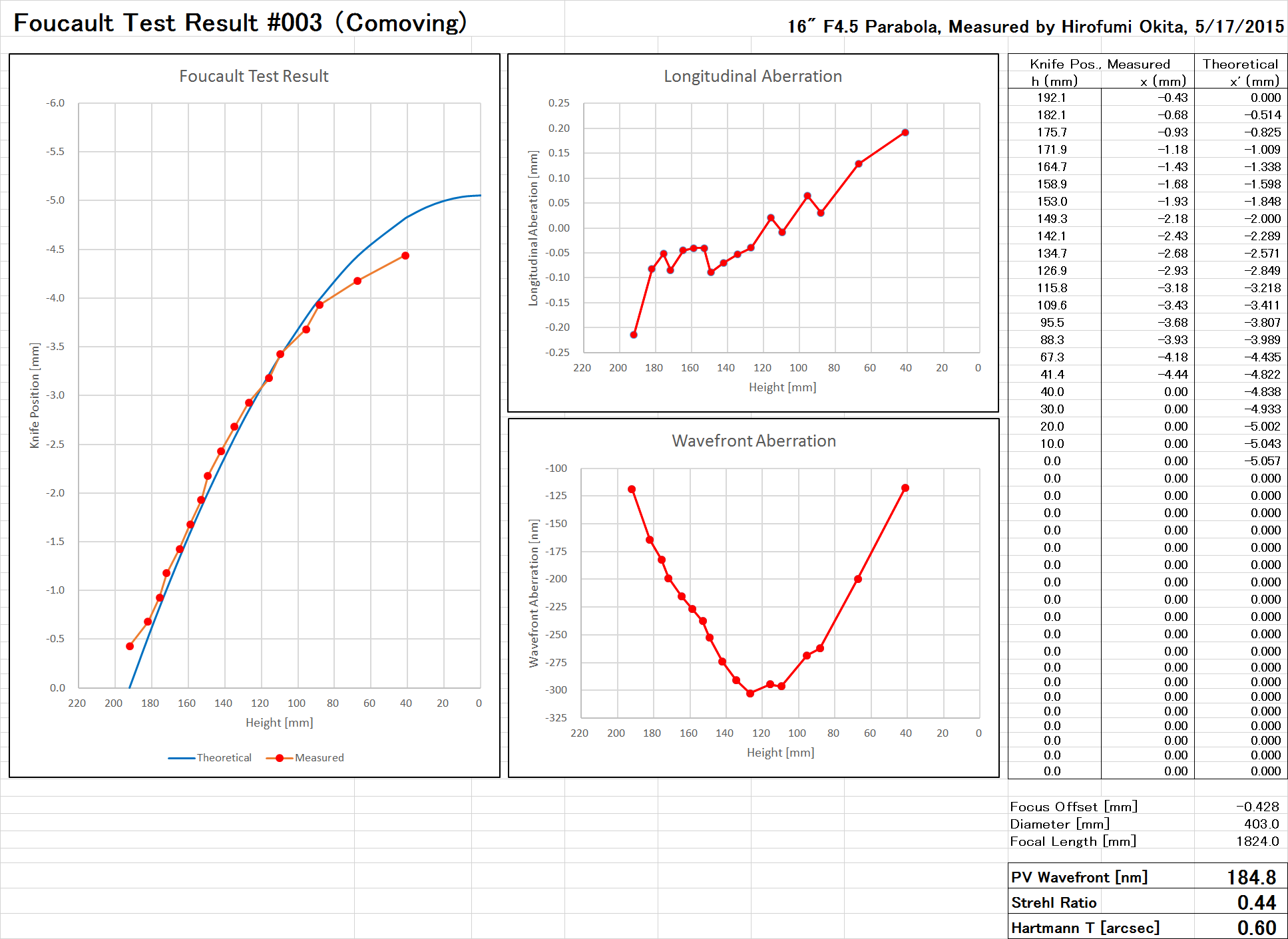
| PV波面誤差 | 184.8 nm (λ/2.7) |
| RMS波面誤差 | 59.3 nm (λ/8.4) |
| PV鏡面誤差 | 92.4 nm (λ/5.4) |
| RMS鏡面誤差 | 29.7 nm (λ/17) |
| ストレール比 | 0.44 |
| ハルトマン定数 | 0.60 |

波長は暗所視比感度のピーク波長である 500 nm で計算しました。 測定の結果から自作40cmドブソニアンの主鏡は単純な「負修正」に近い形状であることがわかりました。 実際に高倍率で明るい恒星を観察すると、確かに焦点内外像は非対称に見え、負修正の傾向が分かります。
しかし不思議とこの程度の精度でもピントが合った位置では星像が肥大しているようには感じませでした。 口径がある程度大きい場合は星像のシャープさは鏡面精度よりもシーイングで決定されるのかもしれません。 ただしこれまで10年間使ってきて 1 度もこの鏡でエアリーディスが見えた経験はなかったため、非常に条件の良いときには鏡の精度不足で細部が見えていなかったのかもしれません。
60cm F3.35 Lockwood Custom Optics
自作60cmドブソニアン で2019年まで使用していた Lockwood Custom Optics 社製 60cm F3.35 主鏡をフーコーテストしました。
| 物理口径 | 610 mm |
| 有効口径 | 605 mm |
| 焦点距離 | 2024 mm (公称値: 79.6") |
| F値 | 3.35 |
| 鏡材 | Supremax |
| 製作者 | Michael E. Lockwood |
| 製作年月日 | 2016年1月4日 |
| シリアルナンバー | #0312 |
| 測定日 | 2016年9月17日 |
| 測定者 | 沖田博文 |
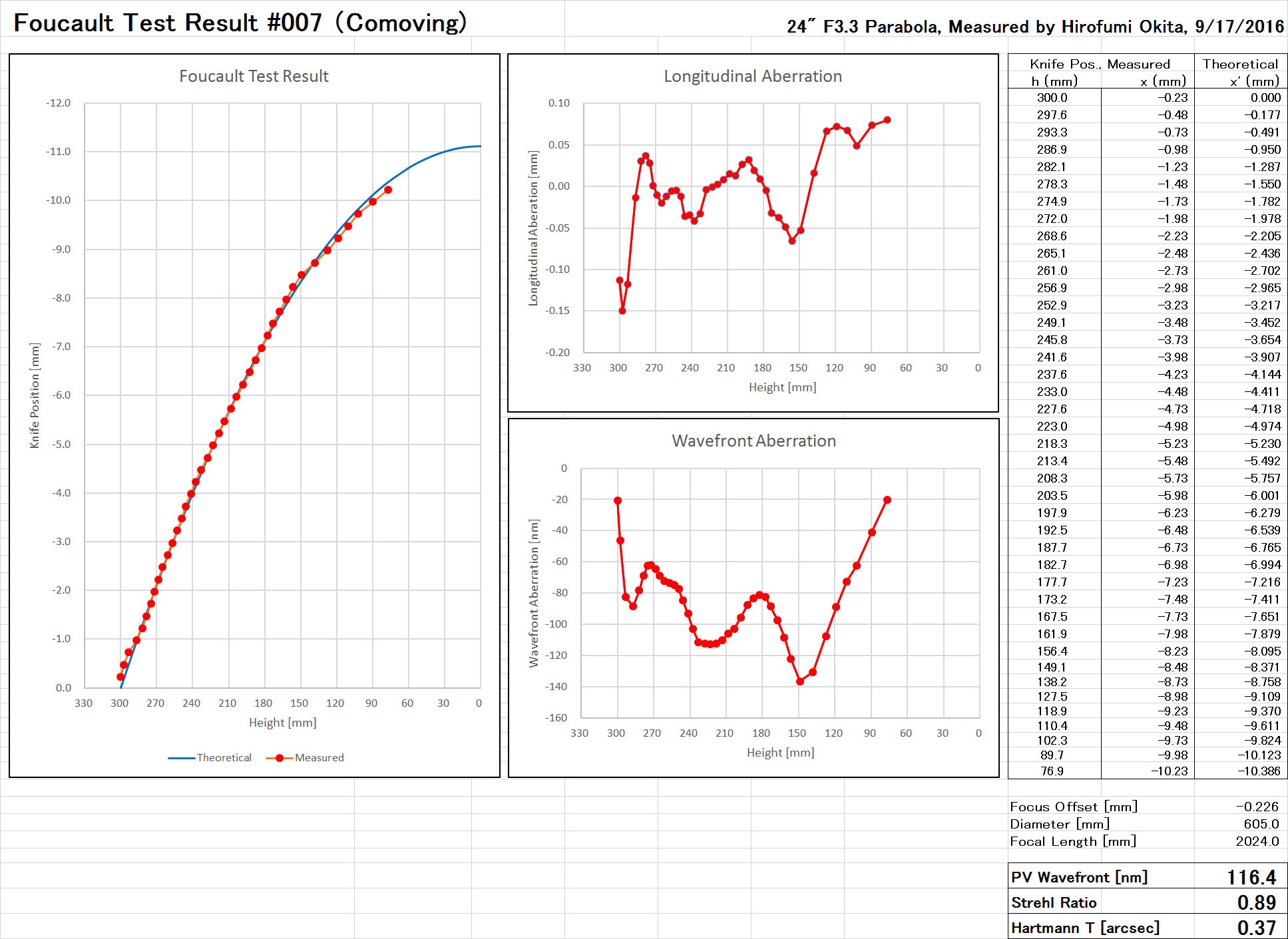
| PV波面誤差 | 116.4 nm (λ/4.3) |
| RMS波面誤差 | 26.0 nm (λ/19) |
| PV鏡面誤差 | 58.2 nm (λ/8.6) |
| RMS鏡面誤差 | 13.0 nm (λ/38) |
| ストレール比 | 0.89 |
| ハルトマン定数 | 0.37 |

波長は暗所視比感度のピーク波長である 500 nm で計算しました。 測定結果からは自作60cmドブソニアンの主鏡は「高次の球面収差」があることが示されました。 実際に高倍率で明るい恒星を見てみると焦点内外像で非対称なのは分かりますが、教科書にあるような単純な負修正・過修正のような星像ではないことが分かります。
また全体として波面誤差が少ないためか、60 cm と口径は大きいのですがシーイングに恵まれた日には800倍以上の高倍率で明るい恒星を観察するとエアリーディスクを見ることができました。 これは40cmドブでは得られなかった経験です。非点収差の検出
自作60cmドブソニアンでは300倍以上の高倍率で明るい恒星を見ると焦点内外像から「非点収差」が認められます。 これまで色々な方法でその原因を探り、定量化を行ってきましたが、主鏡にその原因がある と推定しました。 非点収差の量は、主鏡の焦点距離がある方向とそれと直交する方向とで約 0.07 mm 違うことに相当する程度と見積りました。
ところで非点収差はフーコーテストでも検出が可能なはずです。 たとえば Mike Lockwood's Foucalut Testing Hall of Shame には非点収差がある場合には勾玉のような特徴的な形が見られることが示されています。 鏡を回転させ、非点収差の向きがナイフと 45度 になるとこの特徴的な形が見えるようです。 そこで私も10度刻みに主鏡を回転させて何度もフーコーテストを試みましたが、私の測定では全く検出することができませんでした。
そこで数値的にシミュレートしてみることにしました。 主鏡の焦点距離がある方向とそれと直交する方向とで 0.07 mm 違うと仮定して、フーコーテストでどう見えるか数値的に求めました。 その結果わずかな違いがあることは分かりましたが、0.07 mm では非点収差がない場合とほとんど同じ形になることが分かりました。 0.07 mm の非点収差はフーコーテストで検出することは困難です。
以下にシミュレーション結果を例示します。左側の図が非点収差がない場合、右側の図が非点収差がある場合を表します。灰色の領域はフーコーテストのナイフから +/- 0.01 mm の領域を表し、測定時の室内の気流の影響で曖昧に見える範囲を表しています。

参考のため以下に 0.50 mm の非点収差の場合も示します。
0.50 mm と非点収差が大きい場合には特徴的な形がフーコーテストで見えることが分かりました。

以上をまとめると、自作60cmドブソニアンでは300倍以上の高倍率で非点収差が見られ、その原因は主鏡にあると推定されるが、見積もられる非点収差の量 0.07 mm はフーコーテストでは検出困難である、ということです。 フーコーテストは鏡面形状を測定する強力な技術(光てこ)ですが、ここで示したように限界もあるようです。
その後、製作者の Michael E. Lockwood 氏の協力・助言もあって、主鏡は交換・再製作してもらうことになりました。 交換後の主鏡の非点収差の量は 0.02 mm 程度と約1/4になり、高倍率で見てもほとんど非点収差は知覚できなくなりました。
60cm F3.25 Lockwood Custom Optics(新)
自作60cmドブソニアン では300倍以上の高倍率で明るい恒星を見ると焦点内外像から「非点収差」があることに気が付きました。 色々と実験した結果、原因は主鏡にあると推定し、主鏡は交換・再製作となりました。 交換後の主鏡の非点収差は 約1/4 で高倍率でもほとんど知覚できなくなりました。
以下に自作60cmドブソニアンで2020年から使用中の Lockwood Custom Optics 社製 60cm F3.25 主鏡のフーコーテスト結果を示します。
| 物理口径 | 609.5 mm |
| 有効口径 | 606 mm |
| 焦点距離 | 1967 mm (公称値: 77.45") |
| F値 | 3.25 |
| 鏡材 | Fused Quartz |
| 製作者 | Michael E. Lockwood |
| 製作年月日 | 2019年12月15日 |
| シリアルナンバー | #0421Q |
| 測定日 | 2021年10月16日 |
| 測定者 | 沖田博文 |
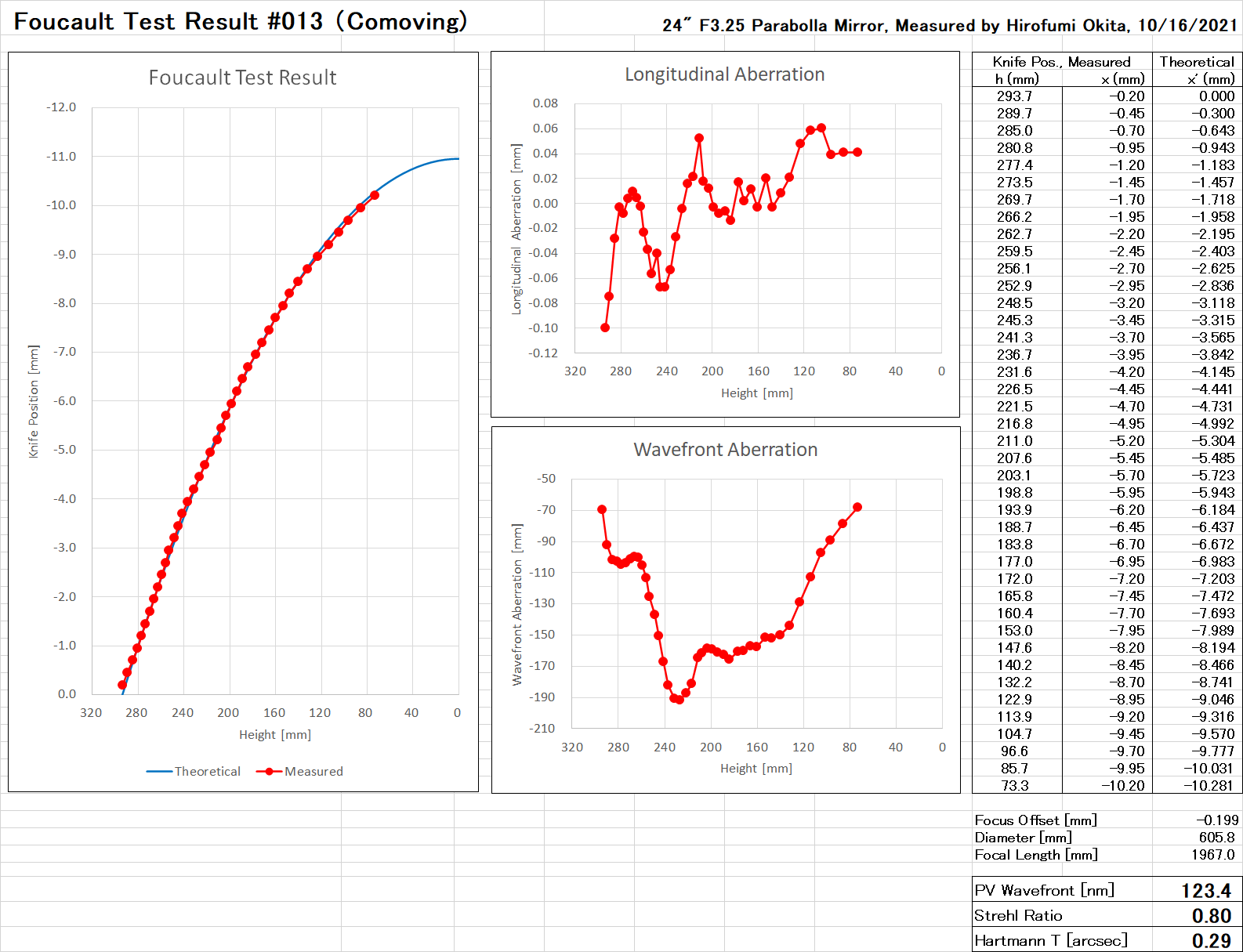
| PV波面誤差 | 123.4 nm (λ/4.1) |
| RMS波面誤差 | 35.2 nm (λ/14.2) |
| PV鏡面誤差 | 61.7 nm (λ/8.1) |
| RMS鏡面誤差 | 17.6 nm (λ/28.4) |
| ストレール比 | 0.80 |
| ハルトマン定数 | 0.29 |

波長は暗所視比感度のピーク波長である 500 nm で計算しました。 測定の結果から前回の鏡よりもPV波面誤差が大きくなった(λ/4.3→λ/4.1)ものの、新しい鏡もレイリー・リミットは満たしていることが分かりました。 実際に高倍率で明るい恒星を見てみると焦点内外像の非対称さは若干大きくなかったかな、と言った程度で、少し球面収差は以前より多いかなと思う程度でした。 一方で非点収差は890倍で見てもほとんど知覚できず全く問題ありません。
15cm F6.71 自作鏡
2019年に鏡面研磨 した 自作15cmドブソニアン の15cm F6.71 自作鏡のフーコーテストを行いました。
| 物理口径 | 152.6 mm |
| 有効口径 | 151.6 mm |
| 焦点距離 | 1016.5 mm |
| F値 | 6.71 |
| 鏡材 | Pyrex |
| 製作者 | 沖田博文 |
| 製作年月日 | 2019年9月22日 |
| シリアルナンバー | #001 |
| 測定日 | 2019年9月25日 |
| 測定者 | 沖田博文 |
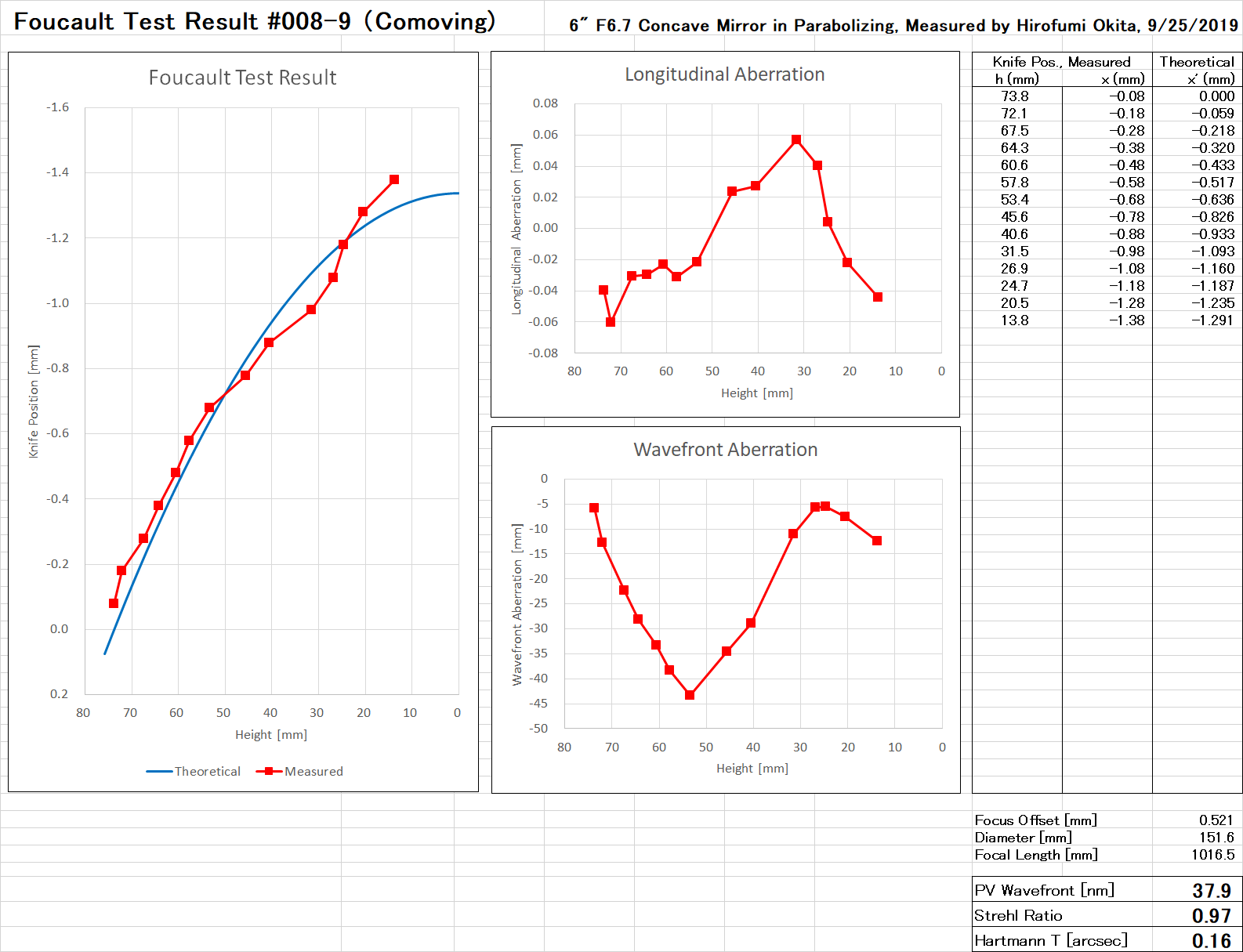
| PV波面誤差 | 37.9 nm (λ/13) |
| RMS波面誤差 | 13.5 nm (λ/37) |
| PV鏡面誤差 | 18.9 nm (λ/26) |
| RMS鏡面誤差 | 6.8 nm (λ/74) |
| ストレール比 | 0.97 |
| ハルトマン定数 | 0.16 |


波長は暗所視比感度のピーク波長である 500 nm で計算しました。 自作15cm鏡はφ55mmよりも外側でほぼ放物面に磨けているものの、φ55mmより内側で負修正、さらにφ30mmよりも内側は深い穴となっているようです。 しかし絶対的なエラー量(縦収差量)は +/-0.06 mm と少なく、PV波面誤差にすると λ/13 と計算され、うまく磨けているように思います。
ただしフーコーテストの画像からは鏡面が荒れていることが分かり、そのためコントラストは悪いかもしれません。 滑らかな鏡面にするには使い古した研磨剤が必要とのことで、丁寧な研磨を心がけましたが初めての自作鏡ではこれ以上は難しいように思います。