ここでは「副鏡のz軸回転」と「副鏡のz軸位置」を調整する手順について考察します。 これらの調整ではサイトチューブを使用します。
サイトチューブとは?
サイトチューブとはレンズの無いアイピース状の形をした筒で、一方の縁の中央にはピンホールがあります。反対側の縁には十字線があるものと無いものが市販されていますが、ニュートン反射の光軸調整を行う場合は十字線があるものを使います。(そのためこのウェブページでは「サイトチューブ+十字線」を単に「サイトチューブ」と呼ぶことにします。)
ただし「副鏡のz軸回転」や「副鏡のz軸位置」の調整には十字線は使いませんので、ここでの調整については十字線は有っても無くてもよいことになります。

何を、どこに合わせるのか?
サイトチューブで副鏡のz軸回転やz軸位置を調整をする場合、サイトチューブを望遠鏡の接眼部に取り付け、中央のピンホールを覗き込み、そこから「直接見える副鏡」と「直接見えるサイトチューブの内壁」とが同心円になるよう、副鏡のz軸回転、副鏡のz軸位置を調整します。 以下の写真のように、サイトチューブを覗くと、視野の中央に副鏡が直接見え、その外側にサイトチューブの内壁が見えることになります。

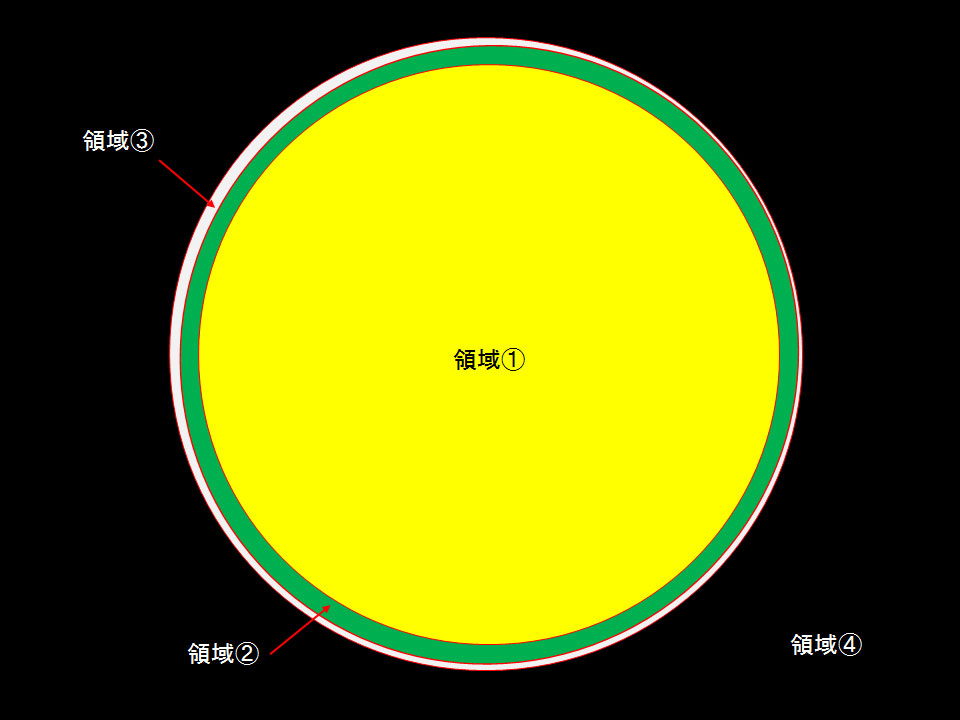
ここで領域 (1) ~ (4) は以下となります。
- 領域 (1):副鏡に写った主鏡
- 領域 (2):直接見える副鏡
- 領域 (3):直接見える副鏡より奥にある鏡筒の壁
- 領域 (4):直接見えるサイトチューブの内壁
よって領域 (2) と領域 (4) とが同心円となるよう調整することになります。
調整の実際
実際に調整を行うとすぐに気が付くのですが、多くの市販の望遠鏡の場合、「副鏡のz軸回転」「副鏡のz軸位置」「副鏡の傾き」を独立に動かす事が出来ないため、調整が困難です。 そこで実際の調整では以下のように行うことになります。
- いったん「副鏡の傾き調整ネジ」を緩め、副鏡が動かせるようにする
- 「副鏡のz軸位置」を調整する
- 「副鏡のz軸回転」を調整する
- 副鏡の傾き調整ネジを締めて「副鏡の傾き」を調整する
- 1 ~ 4 を繰り返し、「直接見える副鏡」と「直接見えるサイトチューブの内壁」とが同心円になるよう調整する
ちなみに 4. の副鏡の傾き調整は サイトチューブ でも行えますが、ズレ量が大きくサイトチューブでは難しいため、私は レーザーコリメーター を使用した方が簡単に行えると思っています。
調整について簡単に書いていますが、実際に行うと結構めんどうな調整となります。 特に「副鏡のz軸回転」は副鏡を回転させても見え方がほとんど変わらないためイマイチうまく調整出来ず、私の場合、悩んでしまいました。
副鏡のz軸回転の解析的理解
そこで「副鏡のz軸回転」について解析的に検討しました。 検討した結果、以下に計算で示すように「副鏡のz軸回転」は「副鏡の傾き」でキャンセル出来ます。 そのため厳密に「副鏡のz軸回転」を調整する必要はありません。
1. 計算の前提条件
解析的に解くため、以下のような前提条件(仮定)を設定し、問題を単純化しました。
- ニュートン反射の光学系(凹面の主鏡と平面の副鏡からなる光学系)について考える
- 副鏡での反射のみを考察する
- 近軸近似を仮定する(つまり sinθ ~ θ、tanθ ~ θ、cosθ ~ 1)
- 主鏡光軸を z 軸とし、それに垂直な軸を x 軸とする
- z 軸、x 軸と垂直な軸を y 軸とする
- z 軸、x 軸、y 軸は副鏡表面のある 1 点で交わる
- 副鏡は xz 平面内で 45 度傾いて置かれているものとする
- 副鏡の x 軸、y 軸、z 軸の回転をそれぞれ θx 、θy 、θz と書く
2. 計算結果
副鏡の法線ベクトル(副鏡に垂直な軸)を考え、これが 3 次元空間で x 軸、y 軸、z 軸に回転した場合にどのようなベクトルになるか考えました。 そして z 軸回転したベクトルが x 軸回転や y 軸回転したベクトルと平行になる解があるかどうか探しました。 以下に計算結果を示します。


よって副鏡の傾きが 45 度の場合、つまり「主鏡の光軸」と「接眼部の光軸」とが直交している場合、「副鏡の z 軸回転」は「副鏡の x 軸回転(yz 平面内の回転)」で打ち消される、すなわち
θz = -θx
となることがわかりました。 これは「副鏡のz軸回転」に誤差があったとしても「副鏡の傾き」で打ち消すことができるということを意味します。
3. 実験とその結果
上記の計算で「副鏡のz軸回転」は「副鏡の傾き」でキャンセルできることが示されましたが、実際の望遠鏡でも実験して確認することにしました。
まず「副鏡のz軸回転」をわざと大きくズラします。 次にこの状態で光軸が合うよう「副鏡の傾き」「主鏡の傾き」を調整します。 そして、サイトチューブを覗くと、次のように見えました。

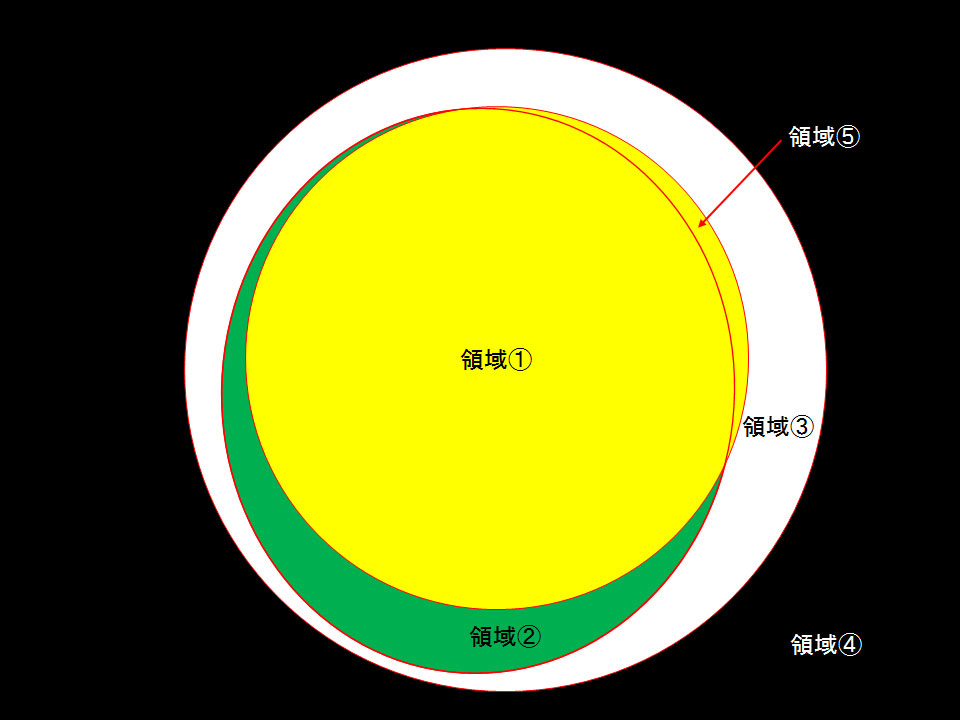
ここで領域 (1) ~ (5) は以下となります。
- 領域 (1):副鏡に写った主鏡
- 領域 (1) + (2):直接見える副鏡
- 領域 (3):直接見える副鏡より奥にある鏡筒の壁
- 領域 (4):直接見えるサイトチューブの内壁
- 領域 (5):本来は副鏡に主鏡が写って見えるはずの領域(副鏡で「ケラれ」ている領域)
「副鏡のz軸回転」の誤差を副鏡の傾きでキャンセルしたため、副鏡が大きく傾いて取り付けられていることがわかります。 次に、この状態でオートコリメーターの中央穴から覗くと、次のように見えました。

さらに、オートコリメーターのオフセット穴から覗くと、次のように見えました。

オートコリメーターの中央穴、オートコリメーターのオフセット穴 から見える主鏡センターマークの位置は共に光軸が合っていることを意味しています。 よって「副鏡のz軸回転」が大きくズレていたとしても「副鏡の傾き」で打ち消すことができ、この状態でも光軸は合わせることが出来ることが実験的にも確かめられました。
4. 副鏡のz軸回転のズレによるケラれ
ただし「副鏡のz軸回転」が大きくズレていて、かつ副鏡サイズがギリギリの場合、主鏡で集めた光に「ケラれ」が生じてしまい、限界等級や分解能が低下してしまいます。
そのため「副鏡のz軸回転」の調整は厳密に合わせる必要はありませんが、「ケラれ」が生じない程度の精度でしっかり調整する必要があります。